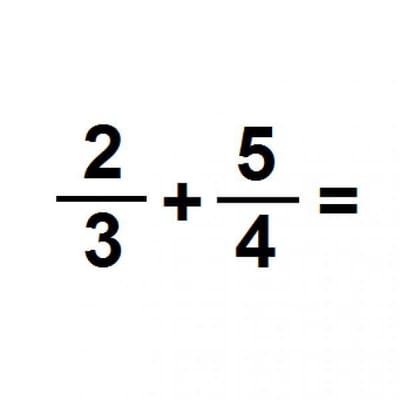Identifica los términos asociados a los números racionales en el siguiente crucigrama.
Más informaciónNúmeros racionales.
Definición, propiedades, ejemplos y operaciones de números racionales.
Avatar: JULIO CESAR "eL MATEMÁTICO"
Definición de números racionales.
Los números racionales son números fraccionarios, sin embargo los números enteros también pueden ser expresados como fracción, por lo tanto también pueden ser tomados como números racionales con el simple hecho de dar un cociente entre el número entero y el número 1 como denominador.
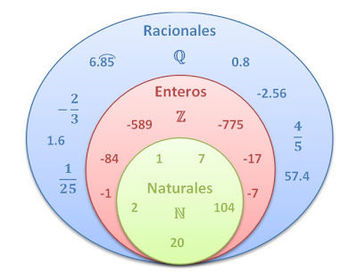
Al conjunto de los números racionales se lo denota con la letra ℚ, que viene de la palabra anglosajona “Quotient” traducción literal de cociente, y que sirve para recogerlos como subgrupo dentro de los números reales y junto a los números enteros cuya denotación es la letra Z. Por ello, en ocasiones se refieren a los números racionales como números ℚ.
Un número racional puede ser expresado de diferentes maneras, sin alterar su cantidad mediante fracciones equivalentes, por ejemplo 1/2 puede ser expresado como 2/4 o 4/8, debido a que estas son fracciones reducibles. Asimismo existe una clasificación de los números racionales dependiendo de su expresión decimal, estos son:
Los números racionales limitados, cuya representación decimal tiene un número determinado y fijo de cifras, por ejemplo 1/8 es igual a 0,125.
Los números racionales periódicos, de los cuales sus decimales tienen un número ilimitado de cifras, pero se diferencian de los números irracionales porque de esas cifras se puede descubrir un patrón definido mientras que en los números irracionales sus cifras decimales son infinitas y no-periódicas.
A su vez los números racionales periódicos se dividen en dos, los periódicos puros, cuyo patrón se encuentra inmediatamente después de la coma, por ejemplo 0,6363636363… y los periódicos mixtos, de los cuales el patrón se encuentra después de un número determinado de cifras por ejemplo 5,48176363636363…
Propiedades de los números racionales.
Propiedad interna.- según la cual al sumar dos números racionales, el resultado siempre será otro número racional, aunque este resultado puede ser reducido a su mínima expresión si el caso lo necesitara.
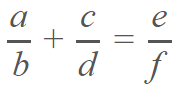
Propiedad asociativa.- se dice que si se agrupa los diferentes sumandos racionales, el resultado no cambia y seguirá siendo un número racional. Veamos:
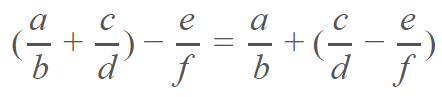
Propiedad conmutativa.- donde en la operación, si el orden de los sumando varía, el resultado no cambia, de esta manera:
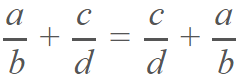
Elemento neutro.- el elemento neutro, es una cifra nula la cual si es sumada a cualquier número racional, la respuesta será el mismo número racional.
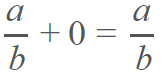
Inverso aditivo o elemento opuesto.- es la propiedad de números racionales según la cual, existe un elemento negativo que anula la existencia del otro. Es decir que al sumarlos, se obtiene como resultado el cero.
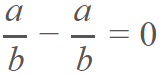
Por otro lado, existen también las propiedades de los números racionales por parte de la multiplicación y la división, y estas son:
Propiedad interna.- en razón de que al multiplicar números racionales, el resultado también es un número racional:
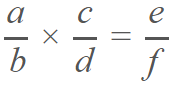Esta además aplica con la división: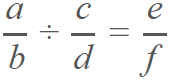
Propiedad asociativa.- donde al agrupar diferentes factores la forma de la agrupación, no altera el producto.
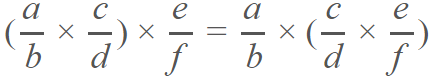
Propiedad conmutativa.- aquí se aplica la famosa frase, el orden de los factores no altera el producto, entre los números racionales también funciona:
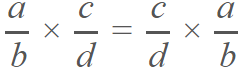
Propiedad distributiva.- al combinar sumas y multiplicaciones, el resultado es igual a la suma de los factores multiplicado por cada uno de los sumandos, veamos el ejemplo:
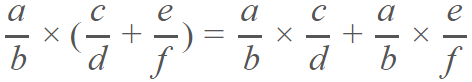
Elemento neutro.- en la multiplicación y la división de números racionales, existe un elemento neutro que es el número uno, cuyo producto o cociente con otro número racional, dará como resultado el mismo número.
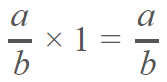
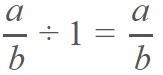
Ejemplos de números racionales.
Los números racionales son números fraccionarios, es decir que podríamos escribir cualquier cociente entre dos números enteros y llamarlo número racional, aquí un ejemplo:
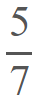Aunque también podría ser expresado de esta manera:
Sin embargo, los números enteros también pueden ser incluidos dentro de los números Q, al formar un cociente con un número neutro, es decir de este modo:
Aunque también podríamos expresar el número entero 3, en forma de fracción, en el caso de necesitarlo en alguna operación matemática, pues al simplificarlo obtenemos la misma respuesta:
También encontramos números racionales enteros negativos, por ejemplo:
0,2424242424… también puede ser tomado como un número racional, pues sus decimales son periódicos, y podemos expresarlo en forma de fracción, así:
Aunque también podría ser expresado de esta manera:Sin embargo, los números enteros también pueden ser incluidos dentro de los números Q, al formar un cociente con un número neutro, es decir de este modo: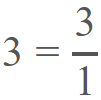Aunque también podríamos expresar el número entero 3, en forma de fracción, en el caso de necesitarlo en alguna operación matemática, pues al simplificarlo obtenemos la misma respuesta: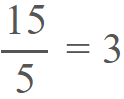También encontramos números racionales enteros negativos, por ejemplo: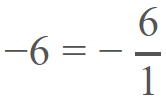0,2424242424… también puede ser tomado como un número racional, pues sus decimales son periódicos, y podemos expresarlo en forma de fracción, así: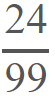
Operaciones con números racionales.
Línea de tiempo de los números Racionales
2000 - 1750 AC
Los babilónicos utilizaban fracciones cuyo denominador era una potencia de 60, mientras que los egipcios usaron, sobre todo, las fracciones con numerador igual a 1. En la escritura, la fracción la expresaban con un óvalo, que significaba parte o partido, y debajo, o al lado, ponían el denominador; el numerador no se ponía por ser siempre 1.
1/01/17501500 - 500 AC
Los griegos y romanos usaron también las fracciones unitarias, cuya utilización persistió hasta la época medieval.
1/01/05001200 - 1300 DC
En el siglo XIII, Leonardo de Pisa, llamado Fibonacci, famoso, entre otras cosas por la serie de Fibonacci, introdujo en Europa la barra horizontal para separar numerador y denominador en las fracciones.
1/01/13001400 - 1500 DC
A principios del siglo XV, el árabe Al Kashi fue el que generalizó el uso de los números decimales tal y como los conocemos hoy.
1/01/15001500 - 1600 DC
A finales del siglo XVI, Simon Stevin desarrolló y divulgó las fracciones decimales que se expresaban por medio de números decimales: décimas, centésimas, milésimas, etc., pero los escribía de una forma complicada; así para 456, 765 escribía 456 (0) 7(1) 6(2) 5(3).
1/01/16001600 - 1700 DC
A principios del siglo XVII, los números decimales ya aparecieron tal y como los escribimos hoy, separando con un punto o una coma la parte entera de la parte decimal.
1/01/17001700 - 1800 DC
Los números decimales se impusieron, en casi todos los países, al adoptarse el Sistema Métrico Decimal, en el siglo XVIII, concretamente en 1792.
1/01/1800Tira cómica: "FRACCIONES ALIENIGENAS"
Actividades prácticas
Analiza la siguiente situación y elige la respuesta correcta.
Más información
Realiza la siguiente operación con números racionales y elige la respuesta correcta.
Más información
Visualiza los ejercicios e identifica la operación de cada uno.
Más informaciónMapa de navegación.
MAPA DE NAVEGACIÓN.
Inicio - Números Racionales. https://racionales.site123.me/
Avatar: JULIO CESAR "EL MATEMÁTICO". https://racionales.site123.me/avatar-julio-cesar-el-matem%C3%81tico
Definición de números racionales. https://racionales.site123.me/definici%C3%B3n-de-n%C3%BAmeros-racionales-1
Propiedades de los números racionales. https://racionales.site123.me/propiedades-de-los-n%C3%BAmeros-racionales
Ejemplos de números racionales. https://racionales.site123.me/ejemplos-de-n%C3%BAmeros-racionales
Operaciones con números racionales. https://racionales.site123.me/operaciones-con-n%C3%BAmeros-racionales
Linea de tiempo de los números racionales. https://racionales.site123.me/l%C3%ADnea-de-tiempo-de-los-n%C3%BAmeros-racionales
Tira cómica: FRACCIONES ALIENÍGENAS. https://racionales.site123.me/tira-c%C3%B3mica-fracciones-alienigenas
Contáctenos. https://racionales.site123.me/cont%C3%A1ctenos
Referencias. https://racionales.site123.me/referencias
Contáctenos
Referencias.
Campus virtual UDES, (2013). “Libro Electrónico Multimedial: Recursos educativos digitales”. Recuperado de: https://aulavirtualeew.cvudes.edu.co/publico/lems/L.000.001.EATE/librov2.html
Números racionales, (2020). Definición de números racionales. Números racionales. [Versión electrónica]. México: Shareaholic, https://numerosracionales.com/
Números racionales, (2020). Propiedades de los números racionales. Números racionales. [Versión electrónica]. México: Shareaholic, https://numerosracionales.com/
Números racionales, (2020). Operaciones de los números racionales. Números racionales. [Versión electrónica]. México: Shareaholic, https://numerosracionales.com/
Números racionales, (2020). Ejemplos de los números racionales. Números racionales. [Versión electrónica]. México: Shareaholic, https://numerosracionales.com/
Campus virtual UDES, (2013). “Libro Electrónico Multimedial: Entornos Virtuales de Aprendizaje”. Recuperado de: https://aulavirtualeew.cvudes.edu.co/publico/lems/L.000.001.EATE/librov2.html
Gomez, Alexander. (2017). "División de números racionales | Fracciones negativas" [en linea]. https://www.youtube.com/watch?v=p_AlfSeIJ8I
Gomez, Alexander. (2017). "Multiplicación de números racionales | Fracciones negativas" [en linea]. https://www.youtube.com/watch?v=myb8EOaK-Nk
Gomez, Alexander. (2018). "Comprendiendo la suma y resta de fracciones | Explicación completa" [en linea]. https://www.youtube.com/watch?v=YpSb9LlsFv8
